Algorithms and Complexity
#1. Finding the kth smallest number
Input: a set X of n distinct numbers and a
number k, 1£k£n.
Output: Find a number x in X such that x is
larger than exactly k-1 elements in X.
#2. Finding an
optimal service route through all edges
Input: A weighted graph G=(V,E)
modeling the map of a city. V is the set of vertices modeling the intersections
of streets. E is the set of edges modeling segments of streets. An edge models
a segment of a street between two insections where there is no other
intersection between these two intersection. Each edge is associated with a
weight modeling the length of the corresponding street segment.
Output: Find the shortest tour (traversal through
a sequence of edges) of G starting from a vertex visiting each edge at
least once and in the end returning to the starting vertex.
Application: Suppose you are given the map of a city
and charged with designing the routes for garbage trucks, snow plows, or
postmen. In all of these applications, every road in the city must be
completely traversed at least once in order to ensure that all deliveries or
pickups are made. For efficiency, you seek to minimize total drive time,
or equivalently, the total distance or number of edges traversed.
#3. Finding an
optimal service route visiting every vertex exactly once
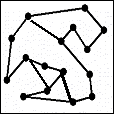

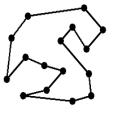
INPUT OUTPUT
Input: A weighted graph G=(V,E) as described in the previous problem.
Output:
Find the shortest tour
(traversal through a sequence of edges) starting from a vextex visiting
all of the vertices of G exactly once and in the end returning to the starting vertex.
#4. Determine
whether a program will finished after a finite number of steps
Input: the source code of a valid program (say,
written in C++) that requires no input from the user when it is run.
Output: Determine whether the program given
unlimited memory space for its use will run to finish after a finite number of
steps.