Homework #10:
Problem #1:
Apply D-matrix algorithm described in the first handout to this
directed graph.
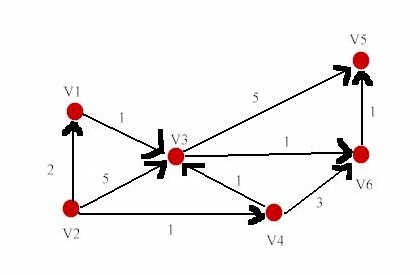
(Please use this fixed vertex order v1, v2, v3, v4,
v5, v6 on rows and columns when you put down the matrices.)
(i)
Write down the matrix D(1) ,
(ii)
Calculate and show matrix D(2) from D(1) and D(1),
(iii)
Calculate and show matrix D(3) from D(2) and D(1),
(iv)
Calculate and show matrix D(4) from D(3) and D(1),
(v)
Calculate and show matrix D(5) from D(4) and D(1),
(vi)
Based on the matrices you got above, what is the minimal path length
over all the paths from v2 to v5 using no more than 2 edges, what is the
minimal path length over all the paths from v2 to v5 using no more than 3
edges, what is the minimal path length over all the paths from v2 to v5 using
no more than 4 edges, what is the minimal path length over all the paths from
v2 to v5 using no more than 5 edges, what is the minimal path length over all
the paths from v2 to v5 using no more than 6 edges respectively?
(vii)
Demonstrate how you can reconstruct a shortest path from v2 to v5
purely based on the matrices D(1) and D(5) without
visual help from the graph above.
Problem #2:
Apply the F matrix algorithm in the
second handout (i.e. the Floyd-Warshall
algorithm) to the directed graph above to calculate and show the matrices (with
the vertex order v1, v2, v3, v4, v5, v6 on rows and columns)
(i)
F(0),
(ii)
F (1),
(iii)
F (2) ,
(iv)
F (3) ,
(v)
F (4) ,
(vi)
F (5) ,
(vii)
F (6).
(viii) Based on the matrices F(0) and F (6) alone
without visual help from the graph above, demonstrate how you can
determine the shortest distance from v2 to v5 and how to reconstruct a shortest
path from v2 to v5. NOTE that the matrices
denoted by the notation F (i)
here are different from the matrices D(i) derived
by the matrix method used in Problem #1.